D+DD Arbeitsbeispiele -
diagramme und nomogramme

... im zeitalter von spreadsheet und taschenrechner?
Diagramme und nomogramme sind nicht einfach grafiken
E+H Duchfluss handbuch
Gegenüberstellung von netz- und leitertafeln
Ein nomogramm für die ferien am meer
Berechnung von kunststoffzahnrädern

See here more work on nomograms by the author

Nomogramme im zeitalter von spreadsheet und taschenrechner?

Genauigkeit	Spreadsheet und taschenrechner täuschen genauigkeit vor – dabei sind die meisten eingabe-daten ungenau. Also was sollen 3 dezimalstellen nach einer langen (näherungs-) rechnung?
Gebrauch	Die batterie ist immer dann leer, wenns am meisten stört. Auf dem bau lebt ein laptop nicht lange, eine dreckige photokopie ist immer noch brauchbar.
Verbreitung	Fachzeitschriften und bücher können nomogramme und diagramme einfach abbilden (aber bitte nicht so verkleinern, dass alle linien zusammen kleben)
Datenlage	Eine komplizierte formel so umstellen, dass die bekannten daten eingegeben werden können, und die unbekannten berechnet werden – das erfordert schon etliches können. Bei empirischen erkenntnissen ist das praktisch unmöglich. Ein nomogramm leistet das gratis und franko: auf der skala anfangen, wo man etwas weiss...

Diagramme und nomogramme sind nicht einfach grafiken

Im gegensatz zu illustrationen und vielen typen von technischen zeichnungen ertragen diagramme und nomogramme keine "türks". Denn dahinter stecken mathematisch exakte oder auch empirisch ermittelte zusammenhänge. Daher werden nomogramme auch rechen-tafeln genannt. Der zeichner muss also hinter die fassade sehen können:

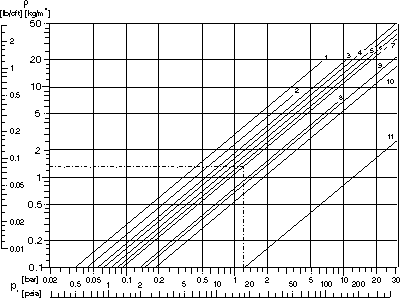
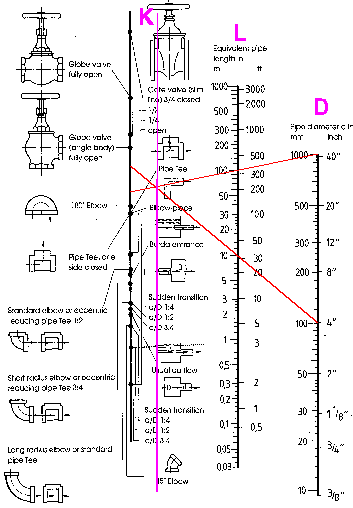Dieses nomogramm zur bestimmung der gleichwertigen rohrlänge von fittings und absperr-organen wird fleissig in der literatur herumgeboten. Es findet sich in firmen-broschüren und auch auf dem web. Dieses nomogamm wurde offenbar mehrmals von vorlagen abgezeichnet, was ich an kleinen unregelmässigkeiten der verschiedenen bilder erkannte. Dieses nomogramm ist schlicht falsch, wie die eingezeichneten roten linien zeigen. Das nomogramm zeigt eine einfache formel: L = K x D bzw K =L/D. K muss also bei 100/1000 und 10/100 dasselbe ergeben (violette zapfenlinie). Der wert K wurde empirisch ermittelt und ist von der oberfläche der fittings (zb grauguss) abhängig. Hier wurden folgende fehler gemacht: Die zapfenlinie K wurde willkürlich verschoben, um platz für die kleinen bildchen zu bekommen. Es fehlt jeder hinweis für die gültigkeit der werte. Woher kommen die verwendeten werte K? Welche rohr-rauhigkeiten liegen zugrunde?

E + H Durchfluss handbuch

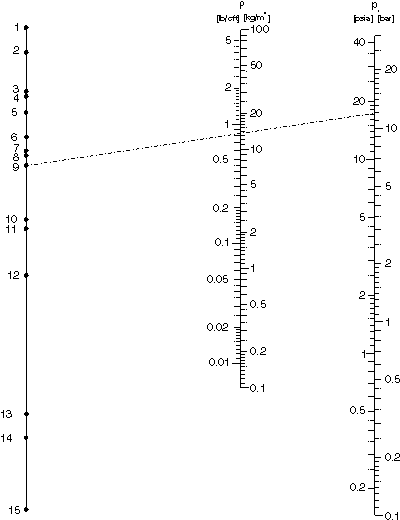
Die firma E+H Flowtec in Reinach brachte ihr Durchfluss-handbuch (ISBN 3-9520220-3-9) neu heraus. Im anhang dieses buches sind über 20 nomogramme (netztafeln und leitertafeln), die D+DD neu zeichnete aufgrund von recherchierten quellen. Das vorgestellte nomogramm sieht in diesem buch folgendermassen aus:

Obenstehendes diagramm trägt das © von Endress + Hauser Flowtec.

Was ist hier nun anders? Den kleinen zeichnungen wurde noch mehr raum gegeben. Demzufolge wurden sowohl die logarithmischen einheiten (abstand zwischen zb 10 und 100 auf einer skala) als auch die lage der leitern und der zapfenlinie neu bestimmt. Das nomogramm gilt für metrische und USA einheiten. Aufgrund einer definierten datenquelle wurden nicht dieselben werte für K und auch nicht dieselben fittings und absperr-organe dargestellt. In der legende zum diagramm wurde die datenquelle angegeben "v.a. nach Crane, Technical Paper No. 410, 1991 (NY, USA)". In den erläuterungen im text steht auch etwas über den gültigkeitsbreich.

Gegenüberstellung von netz- und leitertafel

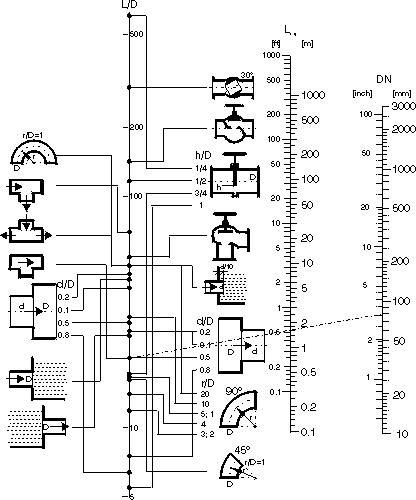
Praktiker wollen oft nezttafeln, weil ihnen diese form einfach geläufig ist. Ein weiterer vorteil gegenüber leitertafeln ist die platzsparende anordnung komplizierter zusammenhänge. In leitertafeln sind für mehr als 2 leitern immer zapfenlinien nötig, was bald einmal zu einem wald von bäumen führt.

Andererseits können leitertafeln wesentlich übersichtlicher sein. Das argument, dass man da ein lineal zum ablesen brauche ist hinfällig: jedes gefaltete papier bildet am knick ein lineal, egal wie gefranst es vorher war...

Dichte verschiedener gase abhängig vom druck

Netztafel	Leitertafel
Obenstehendes diagramm trägt das © von Endress + Hauser Flowtec. Die gase tragen folgende nummern: Acetylen 9   Helium 13   Sauerstoff 6 Ammoniak 10   Kohlendioxyd 4   Schwefeldioxyd 14 Butan 2   Luft 7   Stadtgas 12 Chlor 1   Methan 11   Stickstoff 8 Fluor 5   Propan 3   Wasserstoff 15

Ein nomogramm für die ferien am meer

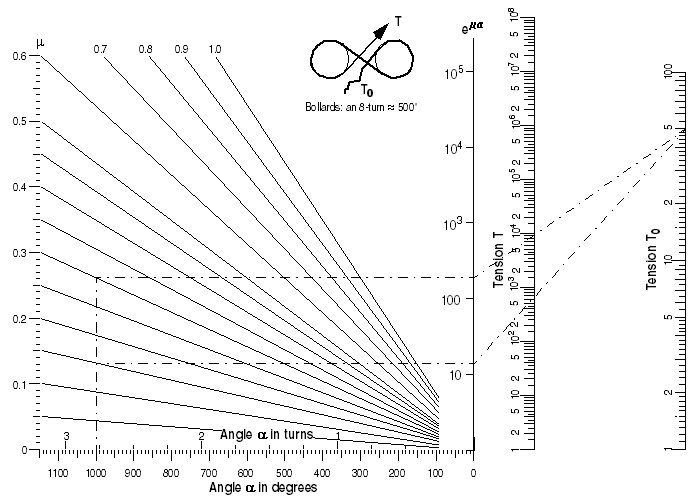
Am hafen sehen Sie die schiffe vertäut. Mit wieviel kraft dürfen wohl die wellen an einem schiff zerren, das mit 2 achter-schlaufen an einem poller festgemacht ist und das lose seil-ende mit einem 70 kg schweren stein am boden festgehalten wird?

Das lose ende des seils wird solcherart mit maximal 50 kg festgehalten. Gemäss skizze im nomogramm ist das seil mit 2 x 500° = 1000° um die beiden poller geschlungen. Damit ergibt sich bei einer reibungszahl µ von 0.3 (textilseil auf gusseisen, trocken) ein 'verstärkungsfaktor' von etwa 200. Daher dürfen die wellen am schiff mit maximal 50 x 200 = 10'000 kg zerren.

An einem kurs-schiff auf dem Zürichsee

Der aufmerksame tourist sieht aber, dass bei diesen pollern höchstens mit 400 grad pro achter-schlaufe gerechnet werden kann. Ausserdem ist am meer sowieso immer alles nass (µ=0.15). Also geht er auf nummer sicher und legt gedanklich noch drei 8-er schlaufen auf. Nun hat er 5 x 400 = 2000 grad umschlingung. 2000 x 0.15 ist dasselbe wie 1000 x 0.3, also ist der verstärkungsfaktor wieder 200. Beruhigt genehmigt sich der feriengast ein gelato oder einen cafe corretto (wir sind offenbar in Italien).

Berechnung von kunststoffzahnrädern

Diese nomgrammsammlung (PDF 390 kB) wurde 1969 in der fachzeitschrift technica veröffentlicht.