Golden rectangle

Golden rectangle

Der goldene schnitt, das rechteck im goldenen schnitt

Proportion d'or, coupe d'or ???

Background
Source
Links

A rectangle with proportions that from classical Greek times has been thought optically pleasing.

The ration of the two sides is approxiamtely 8 : 13 or 1 : 1.625. The exact value of the proportion factor is determined by the formula (sqrt(5) - 1) / 2, giving 1.618033989..

ISO standard 1 : 1.414

Golden rectangle 1 : 1.618

Belletristic books very often are created in these proportions. You can also see this proportion in classical buildings and statues.

Background

The rule to get the proportion (as stated in ancient times) is:

The relation between the shorter and longer side of a golden rectangle is the same as the relation between the larger side to the sum of both lengthes: a : b = b : (a+b)

If this proportion factor is p, then the following formulas demonstrate the very nature of this factor:
p = 1 + 1/p; p² = p + 1

The value p is the limes of quotients of two Fibonacci numbers. Fibonacci numbers f are built up be summing the current number with the predecessor: 1, 1, 2, 3, 5, 8, ... or in a formula f_n+1 = f_n + f_n-1 with f₀ = f₁ = 1.

The proportion factor p = lim f_n / f_n-1 (with n going to infinity):

1/2, 2/3, 3/5, 5/8, 8/13, 13/21, 21/34, 34/55, 55/89, 89/144, 144/233, 233/377, 377/610, 610/987, 987/1597, 1597/2584 2584/4181 4181/6765 ... (See also Fibonacci calculator).

Geometric construction

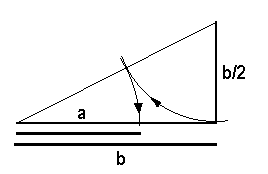
Proportion compas

A special drawing tool to get the proportion immediately may be still in use by artists.

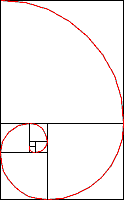
Sideeffects of the Golden Section

Inscribing a square in a golden rectangle leaves another golden rectangle. Setting up quarter circles in each of the squares create very nice spirals (approximations of hyperbolic spirals).

Sources

• Albrecht Beutelspacher und Bernhard, Petri: Der Goldene Schnitt. Spektrum Akademischer Verlag, Heidelberg 1996.
• Spektrum der Wissenschaft, November 1997: Mathematische Unterhaltung.

Further links

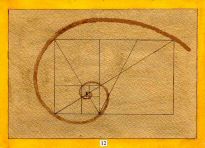
• Artist's rendering of the golden rectangle by Tontyn Hopman in Die Ordnung der Schöpfung in Zahl und Geometrie:
  
• Encyclopedia Britannica
• www.mcs.surrey.ac.uk